PRACTICA11

AMPLIFICADOR OPERACIONAL / OSCILADORES

VIII SEMESTRE ING. ELECTRÓNICA

ELECTRÓNICA III

1.    OBJETIVOS

• Diseñar e implementar osciladores sinusoidales
• Comprobar la aplicación de los operacionales como generadores de señales sinusoidales
• 
  
    MARCO TEÓRICO:
  El oscilador de puente de Wien, tal como aparece en el esquema básico de la f10.3.a, está constituido por un OA en configuración no-inversora de ganancia 1+R2/R1 y unared de realimentación RC cuya función de transferencia es:
  
  
  función de transferencia es:
  
  donde
  
  Sustituyendo 10.9 en 10.8 y operando se obtiene
  
  La ganancia de lazo (ßA) vale
  
  
  
  
  1.    Implemente el siguiente circuito, donde el valor de RA = 1K, RB = 1K Y Ct = 0.1uF
  
  
  
  1.    Realice los cálculos del circuito astable, posteriormente la simulación con las características de la herramienta  Transient / Fourier
  
  
        Start Time: 0S
  
  
  
  
  
  
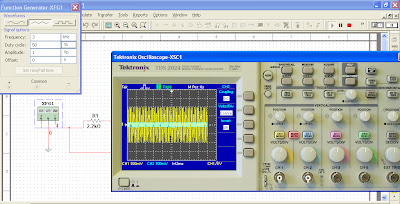
  ·      Stop Time: 1mS
  ·      Step Time: 200nS
  ·      Max. Step: 200nS
  
  
  2.    Visualizar el voltaje de salida del 555.
  a.    ¿Cuanto tiempo permanece encendido el LED?
  b.    ¿Cuál es la frecuencia del voltaje de salida?
  c.    ¿Como compara con lo que predicen las ecuaciones?
  
  
  3.    Coloque un diodo (1N4148) en paralelo con la resistencia RB como se muestra en la figura 2. Visualice el voltaje de salida
  a.    ¿Qué ocurre con la señal de salida comparada con el circuito de la figura inicial? ¿Aumenta o disminuye la frecuencia, y por qué?
  
  
  4.    Agregue un diodo en serie con la resistencia RB, visualice la señal de salida, compare con los resultados obtenidos  en el numerar anterior:
  a.    ¿Qué sucede con la frecuencia y con la forma de onda de salida?
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  a.    ¿Cuanto tiempo permanece encendido el LED?
  
  
  R/= La practica nos arrojo una señal cuadrada que no era uniforme, en alto estaba a 137us y en bajo de 66us, por lo que se puede decir que el LED, permanecía encendido casi todo el tiempo, porque la vista no permite ver la velocidad con la que estaba trabajando la configuración.
  
  
  b.    ¿Cuál es la frecuencia del voltaje de salida?
  
  
  R/= 5.2 KHz
  
  
  c.    ¿Como compara con lo que predicen las ecuaciones?
  
  
  R/= Los cálculos se aproximaron bastante a la simulación y a la practica, tal vez no dieron exactos debido a que en los cálculosno se tiene en cuenta el rango de tolerancia de los materiales utilizados.
  
  
  -       Al colocar un diodo en paralelo con la resistencia R1, la señal de salida se vuelve equitativa, es decir, tanto en alto como en bajo  tienden a tener el mismo tiempo.
  
  
  
  
  
  
  
  
  
  
  

PRACTICA 9

ESCUELA DE INGENIERÍA Y ARQUITECTURA

VIII SEMESTRE ING. ELECTRÓNICA

ELECTRÓNICA III

FILTROS ACTIVOS

1.    OBJETIVOS

• Diseñar e implementar filtros activos de segundo orden
• Comprobar la calidad de la señal de 3dB a la frecuencia de corte en filtros pasa bajas y pasa altas

2.    MARCO TEÓRICO

·         FILTRO BOTTERWORTH

El filtro de Butterworth es uno de los filtros electrónicos más básicos, diseñado para producir la respuesta más plana que sea posible hasta la frecuencia de corte. En otras palabras, la salida se mantiene constante casi hasta la frecuencia de corte, luego disminuye a razón de 20ndB por década (ó ~6n dB por octava), donde n es el número de polos del filtro.

Fue descrito por primera vez por el ingenierobritánico S. Butterworth, (quien rehusó expresamente publicar su primer nombre; se piensa que es Stephen) en su libro "OntheTheory of FilterAmplifiers", WirelessEngineer (también llamado Experimental Wireless and the Radio Engineer), vol. 7, 1930, pp. 536-541.

El filtro de Butterworth más básico es el típico filtro pasa bajo de primer orden, el cual puede ser modificado a un filtro pasa alto o añadir en serie otros formando un filtro pasa banda o elimina banda y filtros de mayores órdenes.

Según lo mencionado antes, la respuesta en frecuencia del filtro es máximamente plana (con las mínimas ondulaciones) en la banda pasante. Visto en un diagrama de Bode con escala logarítmica, la respuesta decae linealmente desde la frecuencia de corte hacia menos infinito. Para un filtro de primer orden son -20 dB por década (aprox. -6dB por octava).

El filtro de Butterworth es el único filtro que mantiene su forma para órdenes mayores (sólo con una caída de más pendiente a partir de la frecuencia de corte).

Este tipo de filtros necesita un mayor orden para los mismos requerimientos en comparación con otros, como los de Chebyshev o el elíptico.

Diseño

Si llamamos H a la respuesta en frecuencia, se debe cumplir que las 2N-1 primeras derivadas de sean cero para Ω = 0y . Únicamente posee polos y la función de transferencia es:

Donde N es el orden del filtro, Ω_c es la frecuencia de corte (en la que la respuesta cae 3 dB por debajo de la banda pasante) y Ω es la frecuencia analógica compleja (Ω=j w).El diseño es independiente de la implementación, que puede ser por ejemplo mediante células de Sallen-Key o Rauch, componentes discretos.

EXPERIMENTO I

1.    Diseñar un filtro pasa bajas de segundo orden Butterworh para una frecuencia de corte de 200Hz

2.    Implementa el circuito previamente diseñado y comprobar su correcto funcionamiento bajo señales sinusoidales de un amplio rango de frecuencia.

DISEÑO FILTRO PASA BAJOS

A_S = 3dB                               F_S = 200Hz

A_P = -40 dB                           F_P = 2KHz

R1 = R2 = 2.2K

se observo que el filtro funciona hasta los 2 KHz que fue diseñado, y posteriormente cambia en esa frecuencia.

EXPERIMENTO II

1.    Diseñar un filtro pasa altas de segundo orden Butterworh para una frecuencia de corte de 2KHz

2.    Implementa el circuito previamente diseñado y comprobar su correcto funcionamiento bajo señales sinusoidales de un amplio rango de frecuencia.

·         RESULTADOS

o   DISEÑO FILTRO PASA BAJOS

A_P = 3dB                               F_P = 2KHz

A_S= -40 dB                            F_S = 200Hz

C1 = C2 = 0.1uF

EXPERIMENTO III

1.    Acoplar los filtros diseñados (el pasa bajas y el pasa altos) para obtener un filtro pasa banda en el rango de 200HZ a 2KHz y comprobar su funcionamiento en un amplio rango de frecuencia.

se realizo la practica, se observo que cuando se llega a 200Hz atenúa la señal hasta los 20KHz y posteriormente deja pasar la señal.

1.    CONCLUSIONES:

·         El filtro pasa bajas activo de segundo orden nos muestra su funcionamiento y comprueba la teoría de que no permite el paso de señales altas

·         El filtro pasa altos activo de segundo orden nos muestra su funcionamiento y comprueba la teoría de que no permite el paso de señales bajas

PRACTICA 8

INGENIERIA ELECTRONICA

VIII SEMESTRE – ELECTRONICA III

INTEGRANTES: DANIEL RIVERA CRUZ

                            MAURO RINCON

TEMA:                 DIFERENCIADOR-INTEGRADOR

LABORATORIO: N°8

1. OBJETIVOS

• Los siguientes experimentos muestran la operación de los circuitos integradores y diferenciadores con opamp a diferentes frecuencias.

2. MARCO TEORICO

3. MATERIALES Y EQUIPOS

• Fuente de Voltaje
• Multímetro
• Generador de funciones
• Osciloscopio

·         Amplificador Operacional LF353N

·         Resistencias 2.2KW (2), 100KW (1), 10 KW (1)

·         Condensadores 4.7nF (1), 20nF (1)

4. PROCEDIMIENTO

 Implementar el siguiente circuito.

Ajuste el voltaje de la señal de entrada triangular a 1Vpp y la frecuencia a 400Hz. ¿Qué se visualiza a la salida?

LA SALIDA EN UNA ONDA CUADRADA

) Mida el voltaje pico negativo de la señal de salida.

-210 mv

) Ahora mida el periodo para el cual el voltaje de la onda cuadrada es negativo ( t1 ).

2.58ms

Vm = -25.9

Ajuste la frecuencia a 1KHz. Repita los pasos anteriores y compare los resultados.

A qué frecuencia cesará el circuito de actuar como diferenciador? 

Voltaje pico negativo de la señal de salida

-395 mv

1.1ms el periodo

Ajuste la frecuencia a 3KHz. Cómo se ve la señal de salida?

Realizar el montaje del siguiente circuito.

Ajuste el Vpp para que la señal de entrada cuadrada sea 1V con f = 10KHz.

 Visualizar la señal de salida.

Mida el voltaje triangular pico a pico.

635mVpp

CONCLUSIONES.

Los anteriores circuitos nos enseñan la operación de los circuitos integradores y diferenciadores con opamp a diferentes frecuencias.

En estos experimentos de laboratorio observarnos  los diferentes comportamientos de estos operacionales.

PRACTICA 7

INGENIERIA ELECTRONICA

INTEGRANTES: DANIEL RIVERA

                         MAURO RINCON

TEMA:               DECTETOR DE NIVEL

1. OBJETIVOS

• Comprobar el funcionamiento del amplificador operacional como detector de cruce por cero

• Comprobar el funcionamiento del amplificador operacional como detector de nivel positivo y negativo

2. MARCO TEORICO

AMPLIFICADOR OPERACIONAL

Un amplificador operacional (comúnmente abreviado A.O. u op-amp), es un circuito electrónico (normalmente se presenta como circuito integrado) que tiene dos entradas y una salida. La salida es la diferencia de las dos entradas multiplicada por un factor (G) (ganancia):
Vout = G·(V₊ − V₋)

El primer amplificador operacional monolítico, que data de los años 1960, fue el Fairchild μA702 (1964), diseñado por Bob Widlar. Le siguió el Fairchild μA709 (1965), también de Widlar, y que constituyó un gran éxito comercial. Más tarde sería sustituido por el popular Fairchild μA741(1968), de David Fullagar, y fabricado por numerosas empresas, basado en tecnología bipolar.

Originalmente los A.O. se empleaban para operaciones matemáticas (suma, resta, multiplicación, división, integración, derivación, etc.) en calculadoras analógicas. De ahí su nombre.

El A.O. ideal tiene una ganancia infinita, una impedancia de entrada infinita, un ancho de banda también infinito, una impedancia de salida nula, un tiempo de respuesta nulo y ningún ruido. Como la impedancia de entrada es infinita también se dice que las corrientes de entrada son cero

3. MATERIALES Y EQUIPOS

• Fuente de Voltaje
• Multímetro
• Osciloscopio
• Generador de funciones

·         Amplificador Operacional LF353N

·         Resistencias R_L=1K

·         Condensadores

·         Protoboard

4. PROCEDIMIENTO

4.1) Como aplicación de los amplificadores operacionales en circuitos comparadores, se desea analizar su operación para tal fin bien sea detector de cruce por cero o detector de  nivel positivo o negativo.

4.2) Implementar el circuito de la figura 1 en donde el voltaje de referencia sea 0V

       La señal Ei es una onda triangular de 1Vpp a 500Hz.

       Ajustar Vcc=10V y -Vee=-10V

4.3) Realizar el análisis teórico de lo que realizará el circuito y graficar la señal de salida que se espera.

4.4) Visualizar en el osciloscopio la señal de salida y compararla con la obtenida teóricamente, existen diferencias?, A qué se deben?

4.5) Ajustar la fuente de voltaje para Vref=0.3V.

4.6) Realizar el análisis teórico y graficar la señal de salida

4.7) Visualizar la señal de salida en el osciloscopio y compararla con la obtenida teóricamente y explicar las diferencias.

4.8) Qué tipo de aplicación se está llevando a cabo?

4.9) Con el Vref=0V Variar la frecuencia de la señal triangular, qué se observa?

4.10) Invertir la polaridad de la fuente de voltaje Vref=-0.3V

Se invierte la señal de salida

4.11) Visualizar en el osciloscopio la señal de salida.

5. CONCLUSIONES

Se comprobó el funcionamiento del operacional como detector de cruce por cero y se observó las diferentes aplicaciones y variaciones de este.

También Se comprobó el funcionamiento del operacional como detector de nivel  positivo y negativo observando igualmente sus respectivas señales de entrada y salida.

Práctica 6 Puente de Wheatstone Amplificador de Instrumentación

1. OBJETIVOS

• Comprobar el funcionamiento del puente de Wheatstone.
• Conocer las características de operación del amplificador de instrumentación y su importancia para acoplar señales de bajo nivel.

2. MARCO TEORICO

Un puente de Wheatstone. es un instrumento eléctrico de medida inventado por Samuel Hunter Christie en 1832, mejorado y popularizado por Sir Charles Wheatstone en 1843. Se utiliza para medir resistencias desconocidas mediante el equilibrio de los brazos del puente. Estos están constituidos por cuatro resistencias que forman un circuito cerrado, siendo una de ellas la resistencia bajo medida.

Figura 1.-Disposición del Puente de Wheatstone.

La Figura 1 siguiente muestra la disposición eléctrica del circuito y la Figura 2 corresponde a la imagen real de un puente de Wheatstone típico.

En la Figura 1 vemos que, R_x es la resistencia cuyo valor queremos determinar, R₁, R₂ y R₃ son resistencias de valores conocidos, además la resistencia R₂ es ajustable. Si la relación de las dos resistencias del brazo conocido (R₁/R₂) es igual a la relación de las dos del brazo desconocido (R_x/R₃), el voltaje entre los dos puntos medios será nulo y por tanto no circulará corriente alguna entre esos dos puntos C y B.

Para efectuar la medida lo que se hace es variar la resistencia R₂ hasta alcanzar el punto de equilibrio. La detección de corriente nula se puede hacer con gran precisión mediante el galvanómetro A.

La dirección de la corriente, en caso de desequilibrio, indica si R₂ es demasiado alta o demasiado baja. El valor de la F.E.M. (E) del generador es indiferente y no afecta a la medida.

Figura 2.- Imagen de un Puente de Wheatstone típico.

Cuando el puente esta construido de forma que R₃ es igual a R₂, R_x es igual a R₁ en condición de equilibrio.(corriente nula por el galvanómetro).

Asimismo, en condición de equilibrio siempre se cumple que:

Si los valores de R₁, R₂ y R₃ se conocen con mucha precisión, el valor de R_x puede ser determinado igualmente con precisión. Pequeños cambios en el valor de R_x romperán el equilibrio y serán claramente detectados por la indicación del galvanómetro.

De forma alternativa, si los valores de R₁, R₂ y R₃ son conocidos y R₂ no es ajustable, la corriente que fluye a través del galvanómetro puede ser utilizada para calcular el valor de R_x siendo este procedimiento más rápido que el ajustar a cero la corriente a través del medidor.

Variantes

Variantes del puente de Wheatstone se pueden utilizar para la medida de impedancias, capacitancias e inductancias

La disposición en puente también es ampliamente utilizada en instrumentación electrónica. Para ello, se sustituyen una o más resistencias por sensores, que al variar su resistencia dan lugar a una salida proporcional a la variación. A la salida del puente (en la Figura 1, donde está el galvanómetro) suele colocarse un amplificador .

3. MATERIALES Y EQUIPOS

·      Fuente de voltaje D.C. (2)

·      Multímetro

·      Opamp LF353N

·      Resistencias 100Ω (3)

·      Trimmer (500Ω)

·      Protoboard

4. PROCEDIMIENTO

4.1) Implementar el siguiente circuito “Puente de Wheatstone”  para R_A=R_B=R_C=100Ω. Estas resistencias deben ser lo más precisas posible (trimmer).

Para R_S se recomienda conectar un trimmer de 500Ω

V=5V

Vi = 547mV

Va = 3.04 V

Vb = 2.49V

Vo = 9.29V

4.4) Acoplar el puente de Wheatstone  con el amplificador de instrumentación como lo indican sus terminales V_a y V_b.

4.5) completar la siguiente tabla.

RS(Ω)	Va	Vb	Vab	Vo	Av
80	2.24 V	2.49V	-0.25 V	-7.49V	29.96
85	2.28V	2.49V	-0.21V	-6.14V	29.23
90	2.38V	2.49V	-0.11V	-3.25V	29.54
95	2.46V	2.49V	-0.03V	-0.92V	30.66
100	2.53V	2.49V	0.04V	-1.02V	25.5
105	2.58V	2.49V	0.09V	2.72V	30.2
110	2.64V	2.49V	0.15V	4.47V	29.08
115	2.70V	2.49V	0.21V	6V	28.57

4.7) Consultar todo acerca de los sensores resistivos RTD, específicamente las PT100, explicar el acople que se realizaría y su funcionamiento al adaptarlo al circuito anteriormente analizado.

Los detectores de temperatura resistivos (RTD – Resistance Temperatura Detector) son sensores de temperatura basados en la variación de la resistencia de un conductor con la temperatura. Su símbolo es el siguiente, en el que se indica una variación lineal con coeficiente de temperatura positivo.

Símbolo RTD

Al calentarse un metal habrá una mayor agitación térmica, dispersándose más los electrones y reduciéndose su velocidad media, aumentando la resistencia. A mayor temperatura, mayor agitación, y mayor resistencia.


La variación de la resistencia puede ser expresada de manera polinómica como sigue a continuación. Por lo general, la variación es bastante lineal en márgenes amplios de temperatura.

donde:

• R₀ es la resistencia a la temperatura de referencia T₀
• ΔT es la desviación de temperatura respecto a T₀ (ΔT = T − T₀)
• α es el coeficiente de temperatura del conductor especificado a 0 °C, interesa que sea de gran valor y constante con la temperatura

5. CONCLUSIONES .

Se comprobó el funcionamiento del puente de Wheatstone.

Conocimos  las diferentes características de operación del amplificador de instrumentación y su importancia para acoplar señales de bajo nivel.